什么是二叉堆
二叉堆就是完全二叉树,或者是靠近完全二叉树结构的二叉树。在二叉树建树时采取前序建树就是建立的完全二叉树。也就是二叉堆。所以二叉堆的建堆过程理论上讲和前序建树一样。
什么是大顶堆、小顶堆
二叉堆本质上是一棵近完全的二叉树,那么大顶堆和小顶堆必然也是满足这个结构要求的。在此之上,大顶堆要求对于一个节点来说,它的左右节点都比它小;小顶堆要求对于一个节点来说,它的左右节点都比它大。
建堆
二叉堆建堆本质上和前序建堆差不多,只不过需要考虑的一点就是大小关系,这一点和二叉搜索树建树有点相似,所以可以得出结论,建树,本质上都是递归建树,只不过因为数据结构的大小要求不一样,需要的判断函数不一样,节点进入哪个位置也不一样。
大顶堆和小顶堆也分为稳定和不稳定的堆。稳定和不稳定指如果具备相同的值,那么他们的插入顺序应该和节点顺序一致。
程序实现
首先,定义出基本的堆结构
|
1
2
3
4
5
6
7
|
public class BinaryHeap {
private Integer value;
private BinaryHeap leftChild;
private BinaryHeap rightChild;
}
|
建堆过程与建二叉树过程一致
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
public static BinaryHeap buildHeap(BinaryHeap binaryHeap, Integer value) {
if (Objects.isNull(binaryHeap)) binaryHeap = new BinaryHeap();
if (Objects.isNull(binaryHeap.getValue())) {
binaryHeap.setValue(value);
return binaryHeap;
}
if (Objects.isNull(binaryHeap.getLeftChild())) {
BinaryHeap binaryHeap1 = new BinaryHeap();
binaryHeap1.setValue(value);
binaryHeap.setLeftChild(binaryHeap1);
} else if (Objects.nonNull(binaryHeap.getLeftChild())) {
if (Objects.isNull(binaryHeap.getRightChild())) {
BinaryHeap binaryHeap1 = new BinaryHeap();
binaryHeap1.setValue(value);
binaryHeap.setRightChild(binaryHeap1);
} else {
// TODO: 2022/1/14 左右节点两种都不为null
if (checkNull(binaryHeap.getLeftChild())) buildHeap(binaryHeap.getLeftChild(), value);
else if (checkNull(binaryHeap.getRightChild())) buildHeap(binaryHeap.getRightChild(), value);
else buildHeap(binaryHeap.getLeftChild(), value);
}
}
return binaryHeap;
}
|
主要原理就是如果当前节点的左节点为空,则把当前值放到左节点,如果左节点不为空,右节点为空,则把值放到右节点。如果左右节点都不为空,就将建树过程转移到下一层,如果左节点有为空的子节点,就转移给左节点,如果左节点没有为空的子节点,且右节点有为空的子节点,那么转移给右节点。如果左右节点都没有为空的子节点,那么也转移给左节点。
以序列2,3,4,5,9,6,8,7为例,按照该算法建立出来的二叉堆结构如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
{
"value": 2,
"left_child": {
"value": 3,
"left_child": {
"value": 4,
"left_child": {
"value": 8,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 7,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 5,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 1,
"left_child": {
"value": 9,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 6,
"left_child": null,
"right_child": null
}
}
}
|
建立大顶堆
大顶堆在建堆的基础上,有一个要求,根节点比左右子树的任何节点的值都大。那么建树的过程可以分为两步,对于每一个值,首先按照建树过程,会到二叉堆的最底部,然后通过不断的让自己与自己的根节点做比较,如果自己大于根节点,就交换自己与根节点的位置,递归回溯即可。
逻辑过程
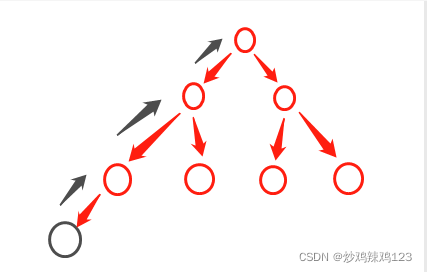
假设现在红色节点组成的已经是一个大顶堆,现在新增了一个节点到这个二叉堆中,而且是比任意节点都大,那么黑色箭头将是该节点的行动路线,它会反复与父级比较,如果大于父级,则交换和父级的关系。
程序实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public static BinaryHeap up(BinaryHeap father) {
if (Objects.nonNull(father.getLeftChild())) {
if (father.getValue() < father.getLeftChild().getValue()) {
int c = father.getValue();
father.setValue(father.getLeftChild().getValue());
father.getLeftChild().setValue(c);
}
up(father.getLeftChild());
}
if (Objects.nonNull(father.getRightChild())) {
if (father.getValue() < father.getRightChild().getValue()) {
int c = father.getValue();
father.setValue(father.getRightChild().getValue());
father.getRightChild().setValue(c);
}
up(father.getRightChild());
}
return father;
}
|
该方法放在普通建树方法之后,就是大顶堆的建树方法了,总的方法如下:
|
1
2
3
4
5
|
public static BinaryHeap bigPush(BinaryHeap binaryHeap, Integer value) {
binaryHeap = buildHeap(binaryHeap, value);
up(binaryHeap);
return binaryHeap;
}
|
还是以序列2,3,4,5,9,6,8,7为例,按照该算法建立出来的大顶堆结构如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
{
"value": 9,
"left_child": {
"value": 8,
"left_child": {
"value": 7,
"left_child": {
"value": 2,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 4,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 3,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 6,
"left_child": {
"value": 1,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 5,
"left_child": null,
"right_child": null
}
}
}
|
建立小顶堆
小顶堆与大顶堆类似
逻辑过程
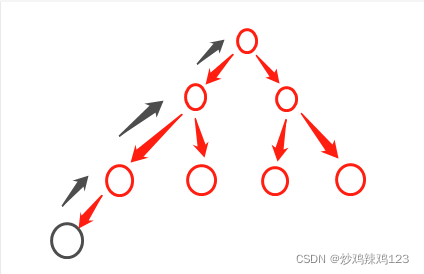
过程与大顶堆一致,不过此时是比父级小就和父级交换。
程序实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public static BinaryHeap down(BinaryHeap father) {
if (Objects.nonNull(father.getLeftChild())) {
if (father.getValue() > father.getLeftChild().getValue()) {
int c = father.getValue();
father.setValue(father.getLeftChild().getValue());
father.getLeftChild().setValue(c);
}
down(father.getLeftChild());
}
if (Objects.nonNull(father.getRightChild())) {
if (father.getValue() > father.getRightChild().getValue()) {
int c = father.getValue();
father.setValue(father.getRightChild().getValue());
father.getRightChild().setValue(c);
}
down(father.getRightChild());
}
return father;
}
|
这个是向下走的过程,最终代码为:
|
1
2
3
4
5
|
public static BinaryHeap smallPush(BinaryHeap binaryHeap, Integer value) {
binaryHeap = buildHeap(binaryHeap, value);
down(binaryHeap);
return binaryHeap;
}
|
以序列2,3,4,5,9,6,8,7为例,按照该算法建立出来的小顶堆结构如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
{
"value": 1,
"left_child": {
"value": 3,
"left_child": {
"value": 4,
"left_child": {
"value": 8,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 7,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 5,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": 2,
"left_child": {
"value": 9,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 6,
"left_child": null,
"right_child": null
}
}
}
|
从堆顶取数据并重构大小顶堆
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public static Integer bigPop(BinaryHeap binaryHeap) {
Integer val = binaryHeap.getValue();
if (binaryHeap.getLeftChild().getValue() >= binaryHeap.getRightChild().getValue()) {
binaryHeap.setValue(binaryHeap.getLeftChild().getValue());
BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getLeftChild().getLeftChild(), binaryHeap.getLeftChild().getRightChild());
up(binaryHeap1);
binaryHeap.setLeftChild(binaryHeap1);
} else {
binaryHeap.setValue(binaryHeap.getRightChild().getValue());
BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getRightChild().getLeftChild(), binaryHeap.getRightChild().getRightChild());
up(binaryHeap1);
binaryHeap.setRightChild(binaryHeap1);
}
return val;
}
public static Integer smallPop(BinaryHeap binaryHeap) {
Integer val = binaryHeap.getValue();
if (binaryHeap.getLeftChild().getValue() <= binaryHeap.getRightChild().getValue()) {
binaryHeap.setValue(binaryHeap.getLeftChild().getValue());
BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getLeftChild().getLeftChild(), binaryHeap.getLeftChild().getRightChild());
down(binaryHeap1);
binaryHeap.setLeftChild(binaryHeap1);
} else {
binaryHeap.setValue(binaryHeap.getRightChild().getValue());
BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getRightChild().getLeftChild(), binaryHeap.getRightChild().getRightChild());
down(binaryHeap1);
binaryHeap.setRightChild(binaryHeap1);
}
return val;
}
|
取出来之后,需要重新调用down或者up函数。以构建小顶堆,取出五次后的结果
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public static void main(String[] args) {
int[] a = new int[]{2, 3, 1, 4, 5, 9, 6, 8, 7};
BinaryHeap binaryHeap = new BinaryHeap();
for (int i = 0; i < a.length; i++) {
binaryHeap = smallPush(binaryHeap, a[i]);
}
System.out.println(Json.toJson(smallPop(binaryHeap)));
System.out.println(Json.toJson(smallPop(binaryHeap)));
System.out.println(Json.toJson(smallPop(binaryHeap)));
System.out.println(Json.toJson(smallPop(binaryHeap)));
System.out.println(Json.toJson(smallPop(binaryHeap)));
System.out.println(Json.toJson(binaryHeap));
}
|
取完后的小顶堆为:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
{
"value": 6,
"left_child": {
"value": 7,
"left_child": {
"value": 8,
"left_child": null,
"right_child": null
},
"right_child": null
},
"right_child": {
"value": 9,
"left_child": null,
"right_child": null
}
}
|