java
☘ 主页 > 软件编程 > java >

Java二叉树的实现和遍历介绍

2022-01-28 | 秩名 | 点击：次

什么是二叉树

简单理解为对于一个节点来说，最多拥有一个上级节点，同时最多具备左右两个下级节点的数据结构。

由于很多排序算法都是基于二叉树实现的，多叉树也是二叉树延伸过去的，所以二叉树的建树和遍历就显得非常重要。

二叉树建树

一般情况是给你一个串，要求让你以前序，中序，后序的方式建树。那么此时我们就需要首先了解三个概念：

我们来看看一棵二叉树的结构：

0

1 2

3 4 5 6

0就是整个二叉树的根节点，1就是0这个节点的左子树，2就是0这个节点的右子树。有了这个知识，我们就可以理解前中后序遍历这个位置属性就是指的根在哪个位置，前序遍历就是根在前，所以就是根左子树右子树的遍历方式；中序遍历就是根在中间，所以就是左子树根右子树的遍历方式；后序遍历就是根在最后，所以就是左子树右子树根的遍历方式。

遍历的方式有三种，对应的建树方式有已知中序和前序建树，已知中序和后序建树，已知前序和后序建树三种。

如果我们仅仅是想构建一棵二叉平衡树，可以简单使用某一种序列建树。用伪代码表示这三种遍历方式就是

1.前序遍历的方式建树

1

2

3

new Tree(根节点);

buildTree(左子树);

buildTree(右子树);

2.中序遍历的方式建树

1

2

3

buildTree(左子树);

new Tree(根节点);

buildTree(右子树);

3.后序遍历的方式建树

1

2

3

buildTree(左子树);

buildTree(右子树);

new Tree(根节点);

前序建树

我们现在以序列 1, 2, 3, 4, 5, 6, 7, 8, 9 为例，如果是前序建树方式，那么二叉树的结构应该为：

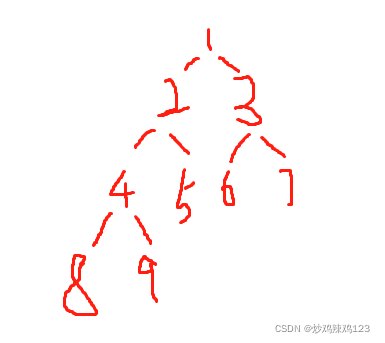
实现也比较简单

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

package com.chaojilaji.book.tree;

 

import com.chaojilaji.auto.autocode.utils.Json;

 

public class Handle {

 

    /**

     * 前序建树

     *

     * @param input

     * @param index

     * @return

     */

    public static Tree buildTreePrologue(int[] input, int index) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

        tree.setValue(input[index]);

        // TODO: 2022/1/12 左右两个节点分别为 2*index-1和2*index+1

        int[] children = new int[]{2 * index + 1, 2 * index + 2};

        if (children[0] < input.length) {

            tree.setLeftChild(buildTreePrologue(input, children[0]));

        }

        if (children[1] < input.length) {

            tree.setRightChild(buildTreePrologue(input, children[1]));

        }

        return tree;

    }

 

 

    public static void demo() {

        int[] a = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9};

        Tree tree = buildTreePrologue(a, 0);

        System.out.println(Json.toJson(tree));

 

    }

 

    public static void main(String[] args) {

        demo();

    }

}

执行结果如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

{

    "value": 1,

    "left_child": {

        "value": 2,

        "left_child": {

            "value": 4,

            "left_child": {

                "value": 8,

                "left_child": null,

                "right_child": null

            },

            "right_child": {

                "value": 9,

                "left_child": null,

                "right_child": null

            }

        },

        "right_child": {

            "value": 5,

            "left_child": null,

            "right_child": null

        }

    },

    "right_child": {

        "value": 3,

        "left_child": {

            "value": 6,

            "left_child": null,

            "right_child": null

        },

        "right_child": {

            "value": 7,

            "left_child": null,

            "right_child": null

        }

    }

}

中序建树

以 1，2，3，4，5，6，7序列为例，如果是中序建树的方式，那么二叉树的结构应该为

代码如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

package com.chaojilaji.book.tree;

 

import com.chaojilaji.auto.autocode.utils.Json;

import com.chaojilaji.auto.autocode.utils.MathUtils;

 

import java.util.LinkedList;

import java.util.Objects;

import java.util.Queue;

 

public class Handle {

 

    /**

     * 中序建树

     * @param input

     * @param height

     * @param maxHeight

     * @return

     */

    public static Tree buildTree2(Queue<Integer> input, int height, int maxHeight) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

 

        if (height < maxHeight) {

            tree.setLeftChild(buildTree2(input, height + 1, maxHeight));

        }

        if (!input.isEmpty()) {

            tree.setValue(input.poll());

        }

        if (height < maxHeight) {

            tree.setRightChild(buildTree2(input, height + 1, maxHeight));

        }

        return tree;

    }

 

    public static void demo() {

        int[] a = new int[]{1, 2, 3, 4, 5, 6, 7};

        Queue<Integer> queue = new LinkedList<>();

        for (int i = 0; i < a.length; i++) {

            queue.add(a[i]);

        }

        Integer maxCeng = new Double(Math.ceil(MathUtils.getLogAN(2, a.length + 1))).intValue();

        System.out.println(Json.toJson(buildTree2(queue, 1, maxCeng)));

    }

 

    public static void main(String[] args) {

        demo();

    }

}

相对前序建树以扩展的方式建立二叉树，中序建树由于无法很好的控制索引，所以这里使用了一个队列来存储整个序列，同时需要算出以当前的节点数，算出建立一棵二叉平衡树，最小的深度为多少。然后按照之前给出的伪代码，按照左根右的方式赋值和递归调用即可。
运行的结果如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

{

    "value": 4,

    "left_child": {

        "value": 2,

        "left_child": {

            "value": 1,

            "left_child": null,

            "right_child": null

        },

        "right_child": {

            "value": 3,

            "left_child": null,

            "right_child": null

        }

    },

    "right_child": {

        "value": 6,

        "left_child": {

            "value": 5,

            "left_child": null,

            "right_child": null

        },

        "right_child": {

            "value": 7,

            "left_child": null,

            "right_child": null

        }

    }

}

后序建树

有了中序遍历，其实后序遍历就非常简单了，以序列1,2,3,4,5,6,7为例，建树应该为

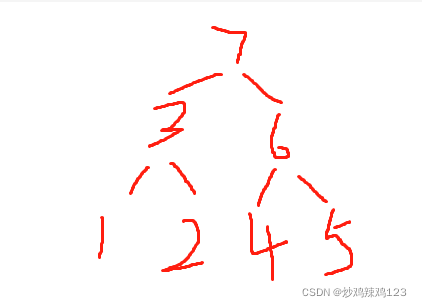
代码如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

package com.chaojilaji.book.tree;

 

import com.chaojilaji.auto.autocode.utils.Json;

import com.chaojilaji.auto.autocode.utils.MathUtils;

 

import java.util.LinkedList;

import java.util.Objects;

import java.util.Queue;

 

public class Handle {

 

    /**

     * 后序建树

     *

     * @return

     */

    public static Tree buildTree3(Queue<Integer> input, int height, int maxHeight) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

 

        if (height < maxHeight) {

            tree.setLeftChild(buildTree3(input, height + 1, maxHeight));

        }

 

        if (height < maxHeight) {

            tree.setRightChild(buildTree3(input, height + 1, maxHeight));

        }

        if (!input.isEmpty()) {

            tree.setValue(input.poll());

        }

        return tree;

    }

 

    public static void demo() {

        int[] a = new int[]{1, 2, 3, 4, 5, 6, 7};

        Queue<Integer> queue = new LinkedList<>();

        for (int i = 0; i < a.length; i++) {

            queue.add(a[i]);

        }

        Integer maxCeng = new Double(Math.ceil(MathUtils.getLogAN(2, a.length + 1))).intValue();                                                    

        System.out.println(Json.toJson(buildTree3(queue, 1, maxCeng)));

 

    }

 

    public static void main(String[] args) {

        demo();

    }

 

 

}

通过分析三个建树方法的代码你可以发现，其实本质上，根赋值代码，与调用左右子树建树函数的摆放的位置不同，就早就了这三种不同的算法。

三种建树方法对应的三种遍历方法本质区别也就是打印值语句与调用左右子树打印值函数的摆放位置不同。如果举一反三的话，我们可以很容易的得出二叉树前中后序遍历的代码。那么，请你自己先尝试一下。

二叉树的遍历

根据建树的经验，知道，我们只需要写出一种遍历方法，那么其他两种遍历方式都有了。区别只不过是换换打印语句的位置。
对于前序遍历，写法如下：

1

2

3

4

5

6

7

8

9

10

11

12

public static void print1(Tree tree) {

    if (Objects.isNull(tree)) return;

    if (Objects.nonNull(tree.getValue())) {

        System.out.print(tree.getValue());

    }

    if (Objects.nonNull(tree.getLeftChild())) {

        print1(tree.getLeftChild());

    }

    if (Objects.nonNull(tree.getRightChild())) {

        print1(tree.getRightChild());

    }

}

那么我们来做一个实验，首先根据序列1,2,3,4,5,6,7利用前序遍历构建出一棵平衡二叉树，然后打印出其前序中序后序遍历的顺序。完整的代码如下：

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

package com.chaojilaji.book.tree;

 

import com.chaojilaji.auto.autocode.utils.Json;

import com.chaojilaji.auto.autocode.utils.MathUtils;

 

import java.util.LinkedList;

import java.util.Objects;

import java.util.Queue;

 

public class Handle {

 

 

    /**

     * 前序建树

     *

     * @param input

     * @param index

     * @return

     */

    public static Tree buildTreePrologue(int[] input, int index) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

        tree.setValue(input[index]);

        // TODO: 2022/1/12 左右两个节点分别为 2*index-1和2*index+1

        int[] children = new int[]{2 * index + 1, 2 * index + 2};

        if (children[0] < input.length) {

            tree.setLeftChild(buildTreePrologue(input, children[0]));

        }

        if (children[1] < input.length) {

            tree.setRightChild(buildTreePrologue(input, children[1]));

        }

        return tree;

    }

 

    /**

     * 中序建树

     *

     * @param input

     * @param height

     * @param maxHeight

     * @return

     */

    public static Tree buildTree2(Queue<Integer> input, int height, int maxHeight) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

 

        if (height < maxHeight) {

            tree.setLeftChild(buildTree2(input, height + 1, maxHeight));

        }

        if (!input.isEmpty()) {

            tree.setValue(input.poll());

        }

        if (height < maxHeight) {

            tree.setRightChild(buildTree2(input, height + 1, maxHeight));

        }

        return tree;

    }

 

    /**

     * 后序建树

     *

     * @return

     */

    public static Tree buildTree3(Queue<Integer> input, int height, int maxHeight) {

        // TODO: 2022/1/12 根节点就是当前index这个节点

        Tree tree = new Tree();

 

        if (height < maxHeight) {

            tree.setLeftChild(buildTree3(input, height + 1, maxHeight));

        }

 

        if (height < maxHeight) {

            tree.setRightChild(buildTree3(input, height + 1, maxHeight));

        }

        if (!input.isEmpty()) {

            tree.setValue(input.poll());

        }

        return tree;

    }

 

    public static void print1(Tree tree) {

        if (Objects.isNull(tree)) return;

        if (Objects.nonNull(tree.getValue())) {

            System.out.print(tree.getValue());

        }

        if (Objects.nonNull(tree.getLeftChild())) {

            print1(tree.getLeftChild());

        }

        if (Objects.nonNull(tree.getRightChild())) {

            print1(tree.getRightChild());

        }

    }

 

    public static void print2(Tree tree) {

        if (Objects.isNull(tree)) return;

        if (Objects.nonNull(tree.getLeftChild())) {

            print2(tree.getLeftChild());

        }

        if (Objects.nonNull(tree.getValue())) {

            System.out.print(tree.getValue());

        }

        if (Objects.nonNull(tree.getRightChild())) {

            print2(tree.getRightChild());

        }

    }

 

    public static void print3(Tree tree) {

        if (Objects.isNull(tree)) return;

        if (Objects.nonNull(tree.getLeftChild())) {

            print3(tree.getLeftChild());

        }

        if (Objects.nonNull(tree.getRightChild())) {

            print3(tree.getRightChild());

        }

        if (Objects.nonNull(tree.getValue())) {

            System.out.print(tree.getValue());

        }

    }

 

    public static void demoPrint() {

        int[] a = new int[]{1, 2, 3, 4, 5, 6, 7};

        Tree tree = buildTreePrologue(a, 0);

        print1(tree);

        System.out.println();

        print2(tree);

        System.out.println();

        print3(tree);

    }

 

    public static void main(String[] args) {

        demoPrint();

    }

}

最终的结果如下：

原文链接：https://blog.csdn.net/xielinrui123/article/details/122628942
相关文章
最新更新