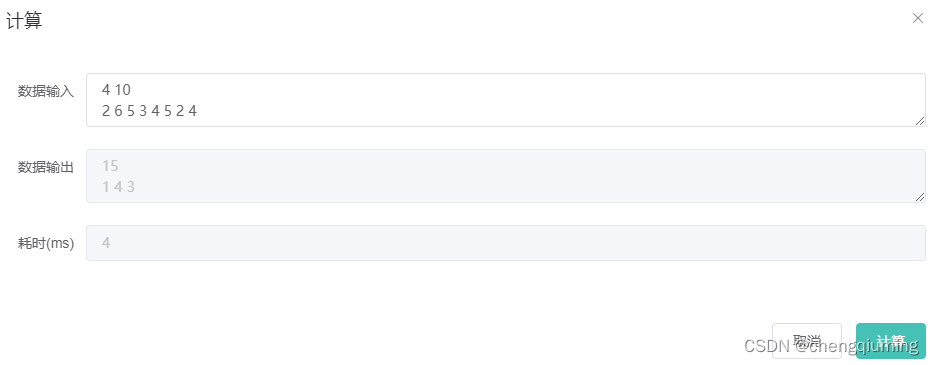
1.问题描述

2.实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 |
package com.platform.modules.alg.alglib.p933;
import java.util.Arrays; import java.util.PriorityQueue;
public class P933 { public static final int N = 10; // 记录最优解 boolean bestx[] = new boolean[N]; // 辅助数组,用于存储排序后的重量和价值 private int w[] = new int[N]; private int v[] = new int[N]; Goods goods[] = new Goods[N]; Object S[] = new Object[N]; // 用来记录最优解 Integer bestp; // 为背包的最大容量 int W; // 为物品的个数。 int n; // 为所有物品的总重量。 int sumw; // 为所有物品的总价值 int sumv; public String output = "";
public P933() { for (int i = 0; i < goods.length; i++) { goods[i] = new Goods(); } for (int i = 0; i < S.length; i++) { S[i] = new Object(); } }
// 计算节点的上界 double Bound(Node tnode) { // 已装入背包物品价值 double maxvalue = tnode.cp; int t = tnode.id; // 排序后序号 double left = tnode.rw; // 剩余容量 while (t <= n && w[t] <= left) { maxvalue += v[t]; left -= w[t++]; } if (t <= n) maxvalue += ((double) (v[t])) / w[t] * left; return maxvalue; }
public String cal(String input) {
String[] line = input.split("\n"); String[] words = line[0].split(" "); // 物品的个数和背包的容量 n = Integer.parseInt(words[0]); W = Integer.parseInt(words[1]); bestp = 0; // 用来记录最优解 sumw = 0; // sumw 为所有物品的总重量。 sumv = 0; // sumv为所有物品的总价值
words = line[1].split(" "); for (int i = 1; i <= words.length / 2; i++) { // 输入每个物品的重量和价值,用空格分开 goods[i].weight = Integer.parseInt(words[2 * i - 2]); goods[i].value = Integer.parseInt(words[2 * i - 1]); sumw += goods[i].weight; sumv += goods[i].value; S[i - 1].id = i; S[i - 1].d = 1.0 * goods[i].value / goods[i].weight; } if (sumw <= W) { bestp = sumv; output = bestp.toString(); return output; } Arrays.sort(S); // 按价值重量比非递增排序 for (int i = 1; i <= n; i++) {//把排序后的数据传递给辅助数组 w[i] = goods[S[i - 1].id].weight; v[i] = goods[S[i - 1].id].value; } priorbfs();//优先队列分支限界法 output += bestp + "\n";
for (int i = 1; i <= n; i++) { // 输出最优解 if (bestx[i]) output += S[i - 1].id + " "; // 输出原物品序号(排序前的) } return output; }
// 优先队列式分支限界法 int priorbfs() { // 当前处理的物品序号t,当前装入背包物品价值tcp,当前剩余容量trw int t, tcp, trw; double tup; // 当前价值上界 tup PriorityQueue<Node> q = new PriorityQueue<>(); // 优先队列
q.add(new Node(0, sumv, W, 1)); // 初始化,根结点加入优先队列 while (!q.isEmpty()) { // 定义三个结点型变量 Node livenode; Node lchild = new Node(); Node rchild = new Node(); livenode = q.peek(); // 取出队头元素作为当前扩展结点 livenode q.poll(); // 队头元素出队 t = livenode.id; // 当前处理的物品序号 // 搜到最后一个物品的时候不需要往下搜索。 // 如果当前的背包没有剩余容量(已经装满)了,不再扩展。 if (t > n || livenode.rw == 0) { if (livenode.cp >= bestp) { // 更新最优解和最优值 for (int i = 1; i <= n; i++) bestx[i] = livenode.x[i]; bestp = livenode.cp; } continue; } if (livenode.up < bestp)//如果不满足不再扩展 continue; tcp = livenode.cp; //当前背包中的价值 trw = livenode.rw; //背包剩余容量 if (trw >= w[t]) { //扩展左孩子,满足约束条件,可以放入背包 lchild.cp = tcp + v[t]; lchild.rw = trw - w[t]; lchild.id = t + 1; tup = Bound(lchild); //计算左孩子上界 lchild = new Node(lchild.cp, tup, lchild.rw, lchild.id); for (int i = 1; i <= n; i++)//复制以前的解向量 lchild.x[i] = livenode.x[i]; lchild.x[t] = true; if (lchild.cp > bestp)//比最优值大才更新 bestp = lchild.cp; q.add(lchild);//左孩子入队 } rchild.cp = tcp; rchild.rw = trw; rchild.id = t + 1; tup = Bound(rchild);//计算右孩子上界 if (tup >= bestp) {//扩展右孩子,满足限界条件,不放入 rchild = new Node(tcp, tup, trw, t + 1); for (int i = 1; i <= n; i++)//复制以前的解向量 rchild.x[i] = livenode.x[i]; rchild.x[t] = false; q.add(rchild);//右孩子入队 } } return bestp;//返回最优值。 } }
// 定义结点。每个节点来记录当前的解。 class Node implements Comparable<Node> { int cp; // cp 为当前装入背包的物品总价值 double up; // 价值上界 int rw; // 剩余容量 int id; // 物品号 boolean x[] = new boolean[P933.N]; // 解向量
Node() { }
Node(int _cp, double _up, int _rw, int _id) { cp = _cp; up = _up; rw = _rw; id = _id; }
@Override public int compareTo(Node o) { return (this.up - o.up) > 0 ? 1 : -1; } }
// 物品 class Goods { int weight; // 重量 int value; // 价值 }
// 辅助物品结构体,用于按单位重量价值(价值/重量比)排序 class Object implements Comparable { int id; // 序号 double d; // 单位重量价值
@Override public int compareTo(java.lang.Object o) { return this.d > ((Object) o).d ? -1 : 1; } } |
3.测试