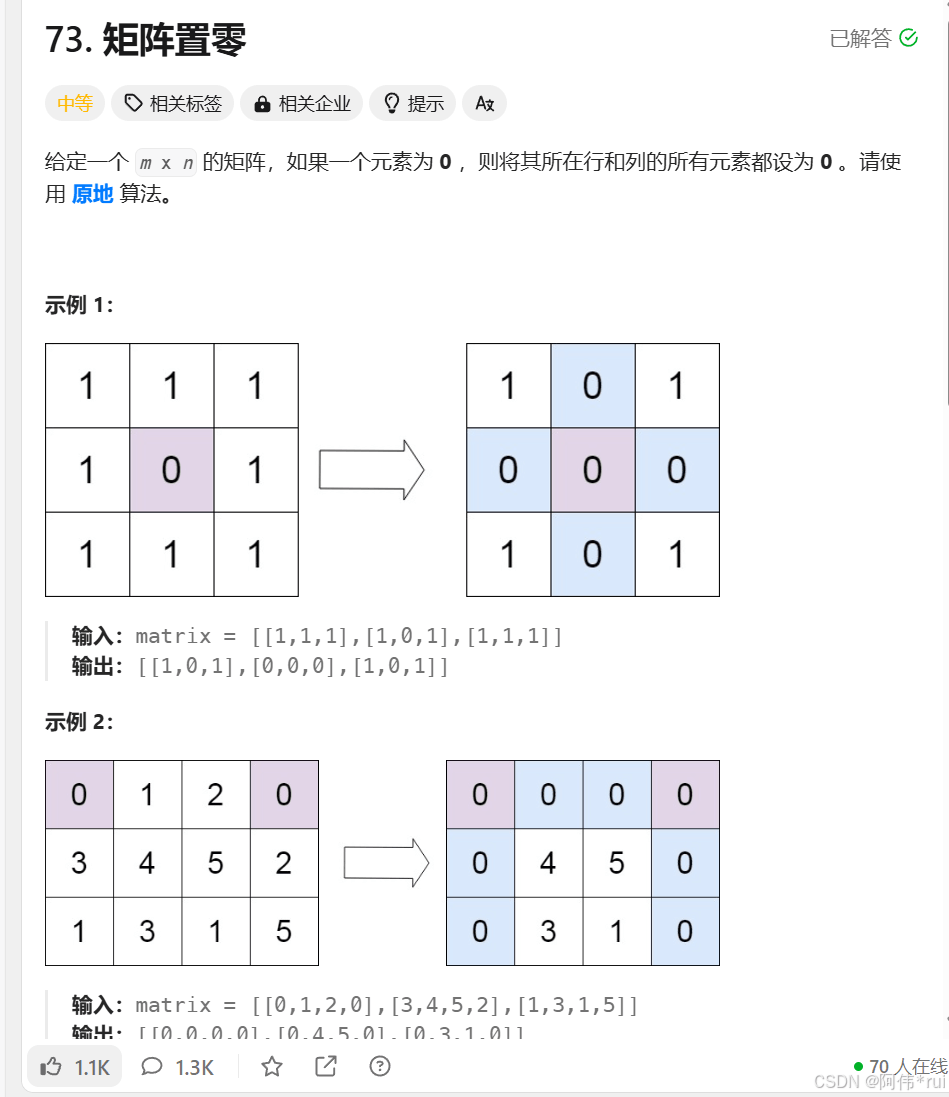
day4 73:矩阵置0
题目:
我的答案:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
ArrayList<Integer> x = new ArrayList<>();
ArrayList<Integer> y = new ArrayList<>();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j]==0){
x.add(i);
y.add(j);
}
}
}
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (x.contains(i)||y.contains(j)){
matrix[i][j]=0;
}
}
}
|
使用集合记录哪一行哪一列含有0,记录下只后,再次遍历矩阵,只要这一行出现0,那么全部就是0,列也是;
题解:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
int m=matrix.length;
int n =matrix[0].length;
boolean x=false;boolean y =false;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][0]==0){
y=true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[0][j]==0){
x=true;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j]==0){
matrix[i][0]=matrix[0][j]=0;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0]==0||matrix[0][j]==0){
matrix[i][j]=0;
}
}
}
if (x){
for (int i = 0; i < n; i++) {
matrix[0][i]=0;
}
}
if (y){
for (int i = 0; i < m; i++) {
matrix[i][0]=0;
}
}
|
题解不再使用额外的数据结构,而是使用变量来标记,这里的主要思路是,利用第一行和第一列来记该行和该列有没有0,因为第一行和第一列被用作标记,所以我们要先记录下来,第一行和第一列有没有0,通过两个循环记录下来,然后遍历整个矩阵,如果一个位置是0,那么这个位置所在行的第一行,和第一列标为0;然后再通过一个循环,如果遍历的位置的第一行或第一列为0那么该位置也为0;然后对第一行和第一列进行处理,如果标记的为0那么第一行或者第一列全部为0;
54:螺旋矩阵

答案:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int left=0;
int right= matrix[0].length-1;
int top=0;
int bottom= matrix.length-1;
ArrayList<Integer> res = new ArrayList<>();
while (left<=right&&top<=bottom){
for (int i = left; i <= right; i++) {
res.add(matrix[top][i]);
}
top++;
for (int j = top; j <=bottom ; j++) {
res.add(matrix[j][right]);
}
right--;
if (top<=bottom){
for (int i = right; i >=left ; i--) {
res.add(matrix[bottom][i]);
} bottom--;
}
if (left<=right){
for (int j = bottom; j >=top ; j--) {
res.add(matrix[j][left]);
}
left++;}
}
return res;
}
|
从左到右,顶部一层遍历完往下移一位,top++;从上到下,遍历完右侧往左移一位,right–;从右到左,判断top <= bottom,即是否上下都走完了。遍历完底部上移,bottom–;从下到上,判断left <= right,遍历完左侧右移,left++;
48-旋转图像

题目要求不能创建新的矩阵。我们先来使用一个矩阵来模拟一下过程:
|
1
2
3
4
5
6
7
8
9
10
11
|
int[][]copy=new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
copy[j][n-i-1]=matrix[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j]=copy[i][j];
}
}
|
具体的规律就是第一行的元素都跑到最后一列按顺序从上到下排序,我们可以找到坐标的规律;

摸索到坐标之间的规律后,我们就要考虑实现题目中的使用原始的矩阵进行旋转;
进行旋转其实是四个元素进行交换位置,就比如四个边角,就是顺时针的交换位置,我们可以总结一下,四个边角坐标之间的关系,然后进行交换位置,需要注意的是需要交换位置的元素有哪些,因为一下就是4个元素,我们需要进行筛选,根据每一行来看,不论奇数还是偶数,只要旋转n/2的行数。根据每一列来看,如果是偶数比如说4列,那么我们只需要旋转前面两列就行,如果是奇数,比如说是5,那么除了1,2列还有第三列要单独处理,所以说要3列也就是n+1/2;
所以:
|
1
2
3
4
5
6
7
8
9
10
|
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1) / 2; j++) {
int temp=matrix[i][j];
matrix[i][j]=matrix[n-j-1][i];
matrix[n-j-1][i]=matrix[n-i-1][n-j-j];
matrix[n-i-1][n-j-j]=matrix[j][n-i-1];
matrix[j][n-i-1]=temp;
}
}
|
然后就是第三种方法,第三种方法使用交换,旋转90度我们可以找到规律就是先是上下翻转,然后是按照对角线进行反转:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n; j++) {
int temp=matrix[i][j];
matrix[i][j]=matrix[n-i-1][j];
matrix[n-i-1][j]=temp;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
int temp=matrix[i][j];
matrix[i][j]=matrix[j][i];
matrix[j][i]=temp;
}
}
|
24-搜索二维矩阵||
题目:

答案:
这题直接遍历搜索也能过;
然后可以优化,比如适用二分查找对每一行数据进行查找;
|
1
2
3
4
5
6
7
|
for (int[] ints : matrix) {
int index = search(ints,target);
if (index>=0){
return true;
}
}
return false;
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public static int search(int[]matrix,int target){
int left=0;
int right=matrix.length;
while (left<=right){
int mid=(right-left)/2+left;
if (matrix[mid]==target){
return mid;
}
if (matrix[mid]>target){
right=mid-1;
}else {
left=mid+1;
}
}
return -1;
}
|
然后还可以从右上角开始检索:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int m =0;
int n =matrix[0].length-1;
while (n>=0&&m<matrix.length){
if (matrix[m][n]==target){
return true;
}
if (matrix[m][n]>target){
n--;
}else {
m++;
}
}
return false;
|
从右上角开始,如果当前值小于目标值就向下遍历,因为下面的大,如果大于目标值就像左移。有点类似于二叉搜索树,左边是左子树,下面是右子树;
206-反转链表
第一种:迭代:
|
1
2
3
4
5
6
7
8
9
|
ListNode pre=null;
ListNode cur=head;
while (cur!=null){
ListNode temp=cur.next;
cur.next=pre;
pre=cur;
cur=temp;
}
return pre;
|
这里需要使用虚拟头节点:
这里先用中间变量记录cur。next,然后反转指针,将指针指向前面的节点。
然后再使pre=cur;
cur=temp
第二种:递归:
|
1
2
3
4
5
6
7
|
if (head==null||head.next==null){
return head;
}
ListNode node = reverseList(head.next);
node.next.next=node;
node.next=null;
return node;
|
234:回文链表
题目:
第一种:双指针:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
List<Integer>res=new ArrayList<>();
while (head!=null){
res.add(head.val);
head=head.next;
}
int l =0;
int r=res.size()-1;
while (l<r){
if (res.get(l)!=res.get(r)){
return false;
}
l++;
r--;
}
return true;
|
先将整个链表的数据加入到集合中,然后再利用双指针进行判断是否是回文子串;
第二种:
|
1
2
|
cur=head;
return reserve(head);
|
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public boolean reserve(ListNode node){
if (node!=null){
if (!reserve(node.next)){
return false;
}
if (cur.val!=node.val){
return false;
}
cur=cur.next;
}
return true;
}
|
将链表放到外部,然后在函数内部递归,使指针遍历到链表的末尾,然后再拿外部的链表和内部的链表末尾进行比较;
141-环形链表
解法1:使用集合判断是否相同:
|
1
2
3
4
5
6
7
8
9
10
11
|
HashSet<ListNode> nodes = new HashSet<>();
ListNode cur=head;
while (cur!=null){
if (!nodes.contains(cur)){
nodes.add(cur);
}else {
return true;
}
cur=cur.next;
}
return false;
|
就是一直遍历,一边遍历,一边将链表的元素加入到集合中,如果发现加入的元素在集合中已经存在了那么就可以说明这是一个环形链表,于是就返回true。如果一直都没有重复的,遍历结束就会返回false
解法2:使用快慢指针,快的走2格,慢的走一格,总会相遇的:
|
1
2
3
4
5
6
7
8
9
10
|
ListNode fast=head;
ListNode slow=head;
while (fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if (fast==slow){
return true;
}
}
return false;
|
就是快慢指针,如果快指针和慢指针是一个元素说明是环形链表;为什么一定相遇呢:这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合。
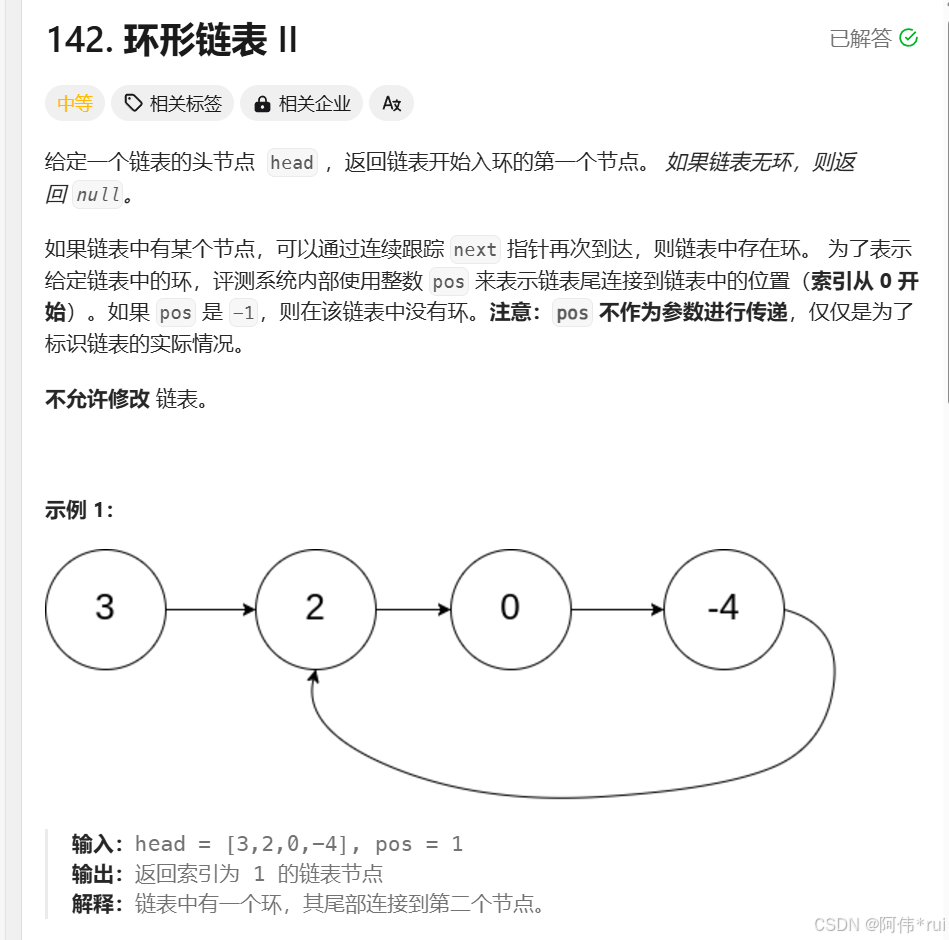
142-环形链表||:
题目:
答案1:
通过集合:
|
1
2
3
4
5
6
7
8
9
10
11
|
HashSet<ListNode> nodes = new HashSet<>();
ListNode cur = head;
while (cur != null) {
if (!nodes.contains(cur)) {
nodes.add(cur);
}else {
return cur;
}
cur=cur.next;
}
return null;
|
当出现重复的元素时就直接返回就行,返回的就是环形的入口元素;
答案2:快慢指针:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
ListNode fast=head;
ListNode slow=head;
while (fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if (fast==slow){
break;
}
}
if (fast==slow){
fast=head;
while (fast!=slow){
fast=fast.next;
slow=slow.next;
}
return fast;
}
return null;
|
在快慢指针重合之后:
我们来讨论一下:f是快指针走的路程。s是慢指针走的路程;
f=s+nb。f=2s。----》s=nb。然后到洞口走的路程的可能是:a+nb;a是环口与链表首部的距离;
相遇的时候s=nb,如果s走a步就是s+nb,正好到环口;
此时我们将快指针放在链表的首部,也走a步也会走到环口,所以当将快指针放到环口时只要快慢指针相遇就是环口的位置;
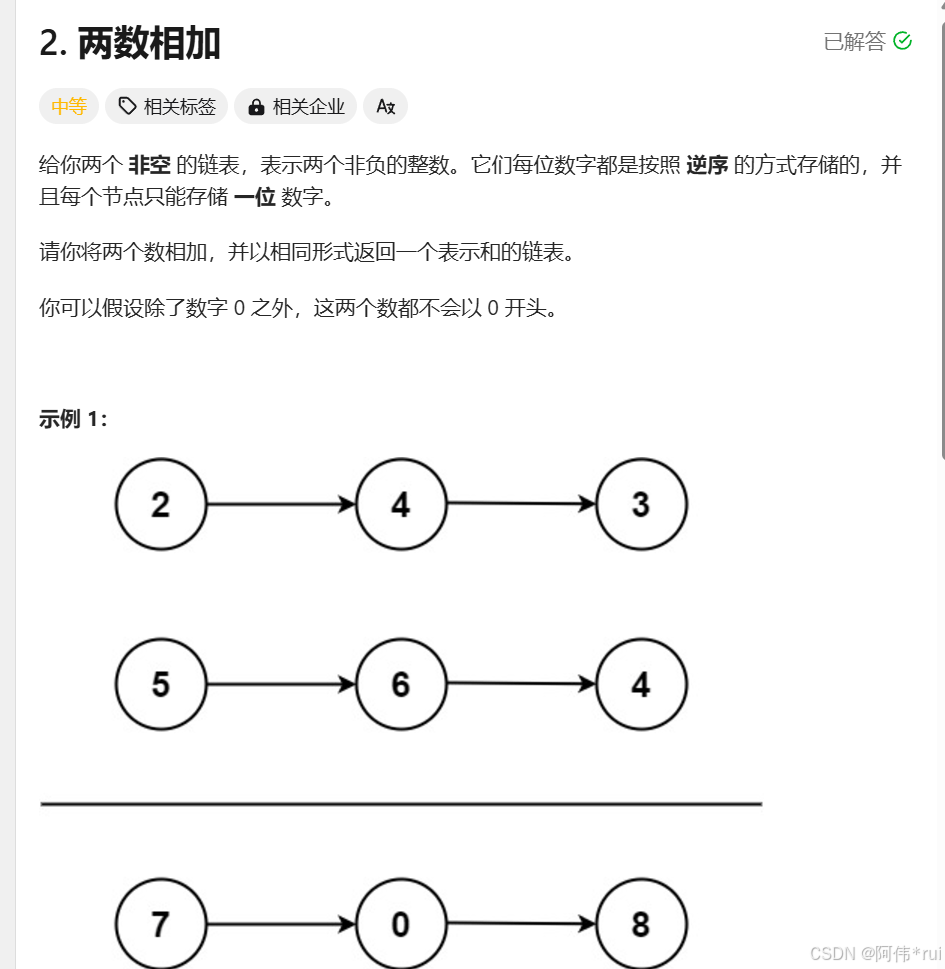
02-两数相加
题目:
答案:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
ListNode sentry = new ListNode(0);
ListNode cur = sentry;
int carry = 0;
while (l1 != null || l2 != null || carry != 0) {
int num1 = l1 != null ? l1.val : 0;
int num2 = l2 != null ? l2.val : 0;
int sum=num1+num2+carry;
carry=sum/10;
ListNode newNode=new ListNode(sum%10);
cur.next=newNode;
cur=newNode;
if (l1!=null)l1=l1.next;
if (l2!=null)l2=l2.next;
}
return sentry.next;
|
由于输入的两个链表都是逆序存储数字的位数的,因此两个链表中同一位置的数字可以直接相加。
我们同时遍历两个链表,逐位计算它们的和,并与当前位置的进位值相加。具体而言,如果当前两个链表处相应位置的数字为 n1,n2,进位值为 carry,则它们的和为 n1+n2+carry;其中,答案链表处相应位置的数字为 (n1+n2+carry)mod10,而新的进位值为 ⌊
10
n1+n2+carry
⌋。
如果两个链表的长度不同,则可以认为长度短的链表的后面有若干个 0 。
此外,如果链表遍历结束后,有 carry>0,还需要在答案链表的后面附加一个节点,节点的值为 carry。
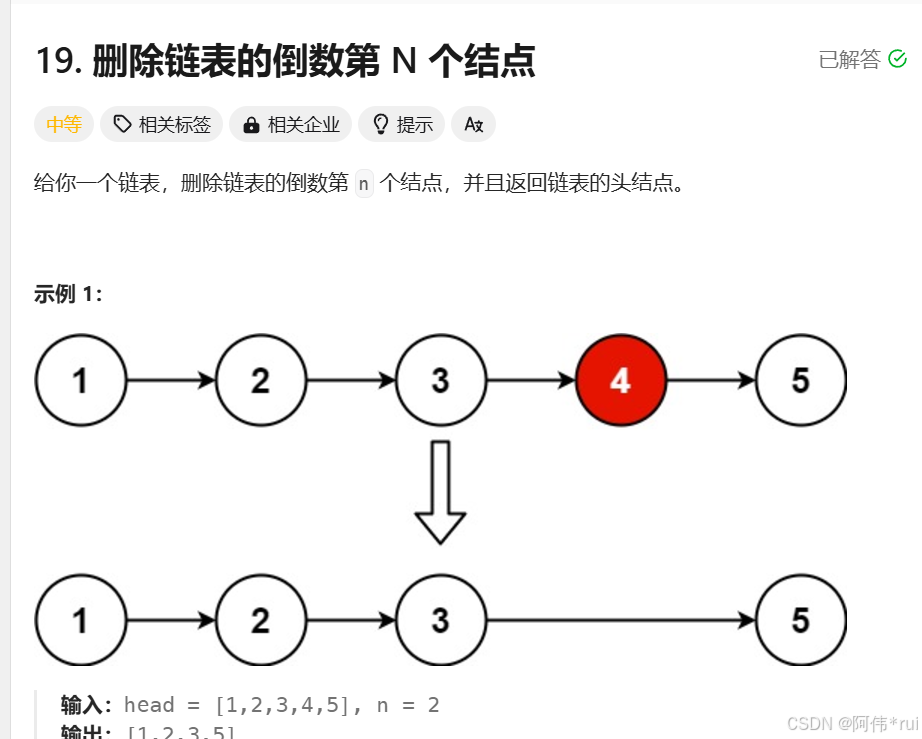
19-删除链表中第n个元素:
题目:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
ListNode fast=head;
for (int i = 0; i < n; i++) {
fast=fast.next;
}
ListNode head1=new ListNode(0);
head1.next=head;
ListNode slow=head1;
while (fast!=null){
fast=fast.next;
slow=slow.next;
}
slow.next=slow.next.next;
return head1.next;
|
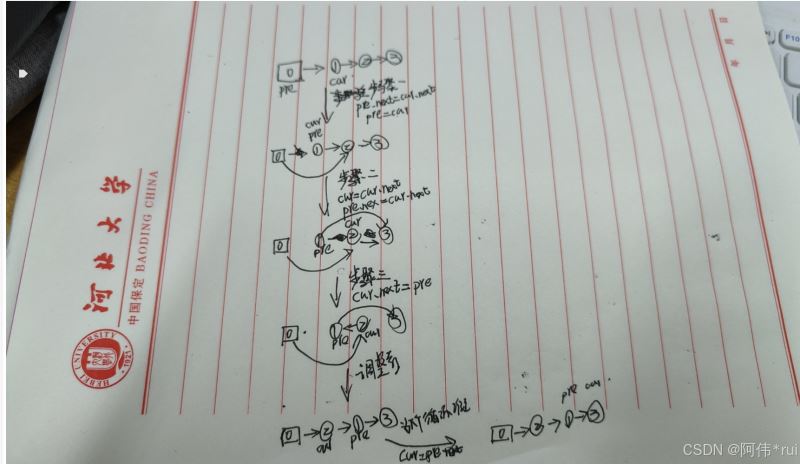
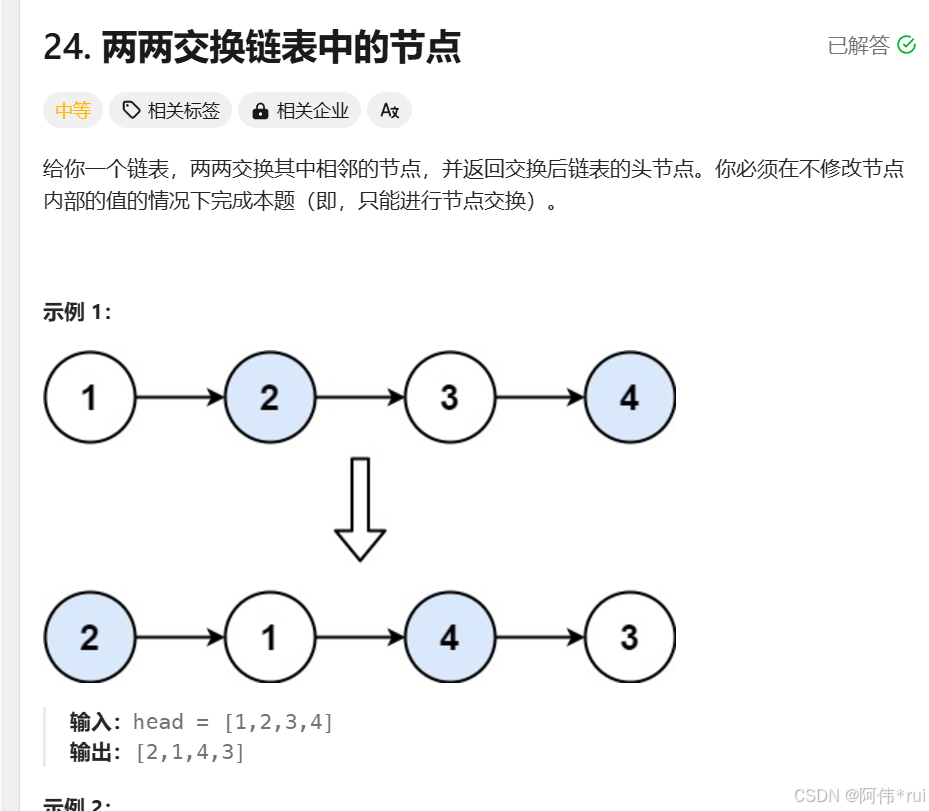
24-两两交换链表的元素
题目:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
if (head==null||head.next==null){
return head;
}
ListNode head0=new ListNode(0);
ListNode pre=head0;
pre.next=head;
ListNode cur=head;
while (cur.next!=null){
pre.next=cur.next;
pre=cur;
cur=cur.next;
pre.next=cur.next;
cur.next=pre;
pre=cur;
cur=cur.next;
}
return head0.next;
|